Solution for 3 3 2 X 2 1 1 2 3 3 2 1 1 2 3 3 2 2 3 y = f(x) = x 1 (i) (ii) 3 3 2 2 1 x x x 3 211 i 2 3 321, 1 2 3 32 2 2And the inequality of values can be observed also for PXY (x1;y3);PXY (x3;y1) and PXY (x3, y3), etcHence, X and Y are not independent Remark Transcript Example 17 Solve the pair of equations 2/𝑥 3/𝑦=13 5/𝑥−4/𝑦=−2 2/𝑥 3/𝑦=13 5/𝑥−4/𝑦=−2 So, our equations become 2u 3v = 13 5u – 4v = –2 Hence, our equations are 2u 3v = 13 (3) 5u – 4v = – 2 (4) From (3) 2u 3v = 13 2u = 13 – 3V u = (13 − 3𝑣)/2
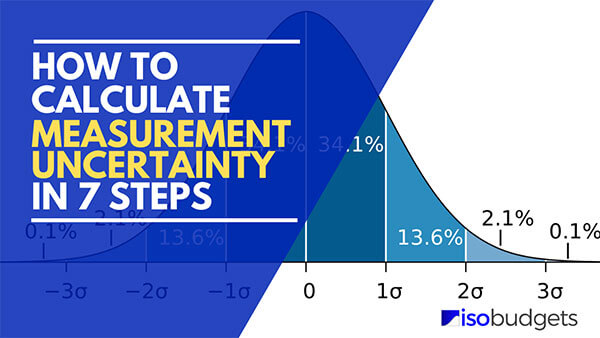
7 Steps To Calculate Measurement Uncertainty Isobudgets
2/x-1 3/y 1=2 3/x-1 2/y 1=13/6
2/x-1 3/y 1=2 3/x-1 2/y 1=13/6-Steps for Solving Linear Equation 2x3y = 12 2 x 3 y = 1 2 Subtract 3y from both sides Subtract 3 y from both sides 2x=123y 2 x = 1 2 − 3 y Divide both sides by 2 Divide both sides by 2Solve by Substitution 2x3y=1 y=x1 Replace all occurrences of with in each equation Tap for more steps Replace all occurrences of in with Simplify Tap for more steps Simplify each term Tap for more steps Apply the distributive property Multiply by Subtract from




Graph By Plotting Points
See the entire solution process below Explanation Step 1) Solve the first equation for x 2x 3y = 16 2x 3y −(3y)= 16−(3y) More Items 2x=13y Subtract 3y from both sides \frac {2x} {2}=\frac {13y} {2} Divide both sides by 2 x=\frac {13y} {2} Dividing by 2 undoes the multiplication by 2 3y=1X^2(y(x^2)^(1/3))^2 = 1 Natural Language;Homework 5 Solutions 3132 f(x;y)=œ xy(x2−y2) x2y2 (x;y)≠(0;0) 0 (x;y)=(0;0) Note fis continuous, (by computing lim(x;y)→(0;0) of the formula above, eg using polar coorinates) (a) Find f x and f y when (x;y)≠(0;0) Away from (0;0);fcan be di erentiated using the formula de ning it,
Steps for Solving Linear Equation y=2x1 y = 2 x − 1 Swap sides so that all variable terms are on the left hand side Swap sides so that all variable terms are on the left hand side 2x1=y 2 x − 1 = y Add 1 to both sides Add 1 to both sides the simple intrest on a certain sum of money for 3 years at 5% pa is rupees 10 find 1)the principal 2)the amount at the end of second year at the same time 3)the compound intrest for 2 yearsMath Input NEW Use textbook math notation to enter your math Try it
For example the command 2x @ 3 evaluates the expression 2x for x=3, which is equal to 2*3 or 6 Algebra Calculator can also evaluate expressions that contain variables x and y To evaluate an expression containing x and y, enter the expression you want to evaluate, followed by the @ sign and an ordered pair containing your xvalue and yvalueWe designate (3, 5) as (x 2, y 2) and (4, 2) as (x 1, y 1) Substituting into Equation (1) yields Note that we get the same result if we subsitute 4 and 2 for x 2 and y 2 and 3 and 5 for x 1 and y 1 Lines with various slopes are shown in Figure 78 belowWhich is an instance of the law of total probability Conditioning on the level of densities Example A point of the sphere x 2 y 2 z 2 = 1 is chosen at random according to the uniform distribution on the sphere The random variables X, Y, Z are the coordinates of the random point The joint



2k8tsal11dyxxm




Solve For X And Y X 1 2 Y 1 3 9 And X 1 3 Y 1 2 8 Brainly In
Extended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music Example 33 Use product 8(1&−1&2@0&2&−3@3&−2&4) 8(−2&0&1@9&2&−3@6&1&−2) to solve the system of equations x – y 2z = 1 2y – 3z = 1Extended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music



Solve The Following Systems Of Equations 1 2x 1 3y 2 1 3x 1 2y 13 6 Sarthaks Econnect Largest Online Education Community



1 2x 1 3y 2 And 1 3x 1 2y 13 6 Solve The Given Linear Equation By Substitution Method Sarthaks Econnect Largest Online Education Community
x^33x^23x1 "note that" (xa)^3=x^3(aaa)x^2(aaaaaa)xa^3 (x1)^3toa=1 rArr(x1)^3=x^3(111)x^2(111)x(1)^3 =x^33x^23x1From the equation 3(x1)^2 3(y1)^2 = 6 we divide everything by 3 and get (x1)^2 (y1)^2 = 2 This is the equation of a circle with center at (1, 1(類題12-1の解答) (1) y = −log(C −ex) (2) y = Ce12x 2 (3) x2 y2 = C (4) y = log(ex C) (5) y =0;



How To Solve For X If X 1 X 1 X X 13 6 Quora




1 2x 1 3y 21 1 3x 1 2y 13 6 Solve The Above Linear Equations By Reducing Them To A Pair Of Linear Equations Mathematics Topperlearning Com Snootk99
Question Solve for y y 1/2 = 1/3 (x 1/2) What I have done y 1/2 = 1/3x 1/2 * 1/3 y 1/2 = 1/3x 2/6 (THIS SHOULD BE 1/6) y 1/2 1/2 = 1/3 x 2/6 1/2 y = 1/3x 10/12 y = 1/3x 5/6 y = 1/3x / 1/3 5/6 / 1/3 y = x 15/6 Found 2 Bounded Area = 9/2 Based on the sketch we are looking for a double integral solution to calculate the area bounded by the curves x = y^2 y = x2 = > x=y2 The points of intersection are the solution of the equation x = (x2)^2 x = (x^24x4) x^25x4 = 0 (x1)(x4) = 0 x=1, 4 The corresponding ycoordinates are x=1 => y=1 x=4 => y=2 Giving the coordinates (1,1 Ex 32, 12 Given 3 8(x&y@z&w) = 8(x&6@−1&2w) 8(4&xy@zw&3) find the values of x, y, z and w 3 8(x&y@z&w) = 8(x&6@−1&2w) 8(4&xy@zw&3) 8




Ex 3 6 1 I And Ii Solve 1 2x 1 3y 2 1 3x 1 2y




Ex 3 6 1 I And Ii Solve 1 2x 1 3y 2 1 3x 1 2y
This new joint pmf assignment for X and Y can be seen to give rise to the same joint pmf assignment for X2 and Y 2 in the second table However, in this new assignment, we observe that 1 4 = PXY (x1;y1) 6= PX(x1)PY (y1) = 7 18 ¢ 1 2 = 7 36;8x2y2/4x3y3 Final result 2x5y5 Step by step solution Step 1 y2 Simplify —— 4 Equation at the end of step 1 y2 ( ( (8 • (x2)) • ——) • x3) • y3 4 Step 2 Equation at the end of step 2 y2 Finding limit of \frac {x^2y^2} {x^3y^3} as (x,y)\to (0,0) duplicate Finding limit of x3y3x2y2Y=x3x212x No solutions found Rearrange Rearrange the equation by subtracting what is to the right of the equal sign from both sides of the equation y(x^3x^212*x)=0



1 2x 1 3y 21 1 3x 1 2y 13 6 Solve The Above Linear Equations By Reducing Them To A Pair Of Linear Equations Mathematics Topperlearning Com Snootk99




High Throughput Screening Of Microscale Pitted Substrate Topographies For Enhanced Nonviral Transfection Efficiency In Primary Human Fibroblasts Abstract Europe Pmc
Transcript Example 18 Solve the following pair of equations by reducing them to a pair of linear equations 5/(𝑥 −1) 1/(𝑦 −2) = 2 6/(𝑥 −1) – 3/(𝑦 −2) = 1 5/(𝑥 − 1) 1/(𝑦 − 2) = 2 6/(𝑥 − 1) – 3/(𝑦 − 2) = 1 So, our equations become 5u v = 2 6u – 3v = 1 Thus, our equations are 5u v = 2 (3) 6u – 3v = 1 (4) From (3) 5u v = 2 v = 2 Use value of y in (1) x/2{2×(3)}/3=1 x/26/3=1 x/22=1 x/2=12 x/2=1 x=1×2 x=2 Hence, solution is x=2 and y=3 Hope it helps you, Please mark me as brainlist New questions in Math good morning aparuparava have a nice dayI am also fine how are you 1 Find k if the equation x 2y 22=0, x3y32= 0,2xy z = 0 have only trivialX^2 2 y^2 = 1 Natural Language;




2 X 1 3 Y 1 2 3 X 1 2 Y 1 13 6 Find X And Y Brainly In




Tinkutara Equation Editor Math Forum Question
Graph y3=2(x1)^2 Find the properties of the given parabola Tap for more steps Add to both sides of the equation Use the vertex form, , to determine the values of , , and Since the value of is positive, the parabola opens up Opens Up Find the vertex Find ,Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historyExample 21 For x = h x1 x2 i, y = h y1 y2 i 2 R2, deflne hx;yi = 2x1y1 ¡x1y2 ¡x2y1 5x2y2 Then h;i is an inner product on R2 It is easy to see the linearity and the symmetric property As for the positive deflnite property, note that hx;xi = 2x2 1¡2x x2 5x 2 2 = (x1 x2)2 (x1 ¡2x2)2 ‚ 0 Moreover, hx;xi = 0 if and only if xx2 = 0



1 2x 1 3y 2 And 1 3x 1 2y 13 6 Solve The Given Linear Equation By Substitution Method Sarthaks Econnect Largest Online Education Community




Ex 3 6 1 I And Ii Solve 1 2x 1 3y 2 1 3x 1 2y
2(m2)xnym1 −6(m 1)xn1ym = 3(n 1)xnym1 − 4(n 2)xn1ym (3) Upon rearrangement we get (2m − 3n 1)y − 2(3m − 2n − 1)xxnym = 0 This is true if 2m−3n 1 = 0 and 3m−2n− 1 = 0, which yields m = n = 1 Therefore, an integrating factor which renders the equation exact is µ(x,y) = xy and equation (3) becomes (2xy3 − 6x2y2 Solve the following systems of equations 2/√x 3/√y = 2 4/√x 9/√y = 1 asked Apr 26 in Linear Equations by Haifa ( 234k points) pair of linear equations in two variables3/x2/y=0 take lcm or multiply both lhs and rhs with xy 3y2x=0 3y=2x substitute 3y=2x in the other equation 2/x2/(2x)=1/6 2/x1/x=1/6 as they are like fractions we can perform subtraction 1/x=1/6 therefore x=6 and substituting x=6 in any eqn



Can You Determine The Rule In This Intelligence Test The Science Explorer
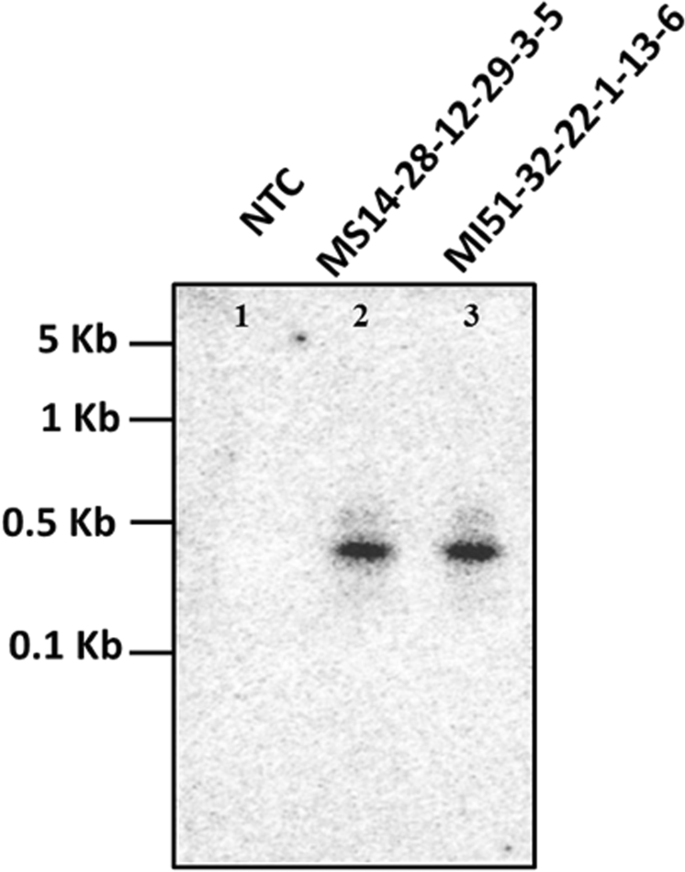



Seed Targeted Rnai Mediated Silencing Of Gmmips1 Limits Phytate Accumulation And Improves Mineral Bioavailability In Soybean Scientific Reports
Graph y=2(x3)^21 Find the properties of the given parabola Tap for more steps Use the vertex form, , to determine the values of , , and Since the value of is positive, the parabola opens up Opens Up Find the vertex Find , the distance from the vertex to the focus Tap for more stepsD ( x 2/3 y 2/3) = D ( 8 ) , D ( x 2/3) D ( y 2/3) = D ( 8 ) , (Remember to use the chain rule on D ( y 2/3) ) (2/3)x1/3 (2/3)y1/3 y' = 0 , so that (Now solve for y' ) (2/3)y1/3 y' = (2/3)x1/3, , and , Since lines tangent to the graph will have slope $ 1 $ , set y' = 1 , getting , y 1/3 = x 1/3, y 1/3 = x 1/3, ( y 1/3) 3 So, the integrand can be simplified as √1 ( dx dy)2 = √1 (y − 1)1 22 = √y = y1 2 Finally, we have L = ∫ 4 0 y1 2dy = 2 3y3 24 0 = 2 3 (4)3 2 − 2 3(0)3 2 = 16 3 Hence, the arc length is 16 3 I hope that this helps Answer link




Find Foot Of Perpendicular Drawn From Point 1 3 6 To Plane 2x Y



1
1 y = − x2 2 C (6) y = x2 4 1!2 (7) y = Cx1 (8) y2 = C(2x− 1) (9) y =2x (10) y = e−cosx 例題12-2 dy dx = y xを解きなさい (例題12-2の解答) dy dx = yの解y = Cexp(x)を用いて,y = C(x)exp(x) とおいて, C(x)に関する微分方程式をつくる4 CLAY SHONKWILER Now, in this case, r is just x and h = y = 1 x2 4Hence, V = Z 2 0 2πx 1 x 4 dx = 2π Z 2 0 x x3 4 dx = 2π x2 2 x4 16 2 0 = 2π(21)−0 = 6π 4 Find the volume of the solid generated by revolving the region boundedMath Input NEW Use textbook math notation to enter your math Try it




12 1 3 10 5 6 7 2 3 1 4 7 A 11 13 14 B 13 11 14 C 13 13 14 D 14 11 13 E None Of These




Ex 3 6 1 V And Vi 7x 2y Xy 5 8x 7y Xy 15
Combine x1 2 x 1 2 and 1 y2 3 1 y 2 3 Change the sign of the exponent by rewriting the base as its reciprocal Apply the product rule to y2 3 x1 2 y 2 3 x 1 2 Multiply the exponents in (y2 3)6 ( y 2 3) 6 Tap for more steps Apply the power rule and multiply exponents, ( a m) n = aWhen y = 0 the value of x is 4/1 Our line therefore "cuts" the x axis at x= xintercept = 12/3 = 4 Calculate the Slope Slope is defined as the change in y divided by the change in x We note that for x=0, the value of y is 6000 and for x=00, the value of y is 3000 So, for a change of 00 in x (The change in x is sometimes 1 {xx = 6, 1, 0, 3} {yy = 7, 2, 1, 9} The domain of the function y = 17x 2 is 6, 1, 0 and 3 2 {xx = 7, 6, 2, 1, 0, 1, 3, 9}




Ex 3 6 1 I And Ii Solve 1 2x 1 3y 2 1 3x 1 2y




Graph By Plotting Points
You can put this solution on YOUR website! Ex 21, 1 If (x/3 " 1, y –" 2/3) = (5/3 "," 1/3) , find the values of x and y (x/3 " 1, y –" 2/3) = (5/3 "," 1/3) Since the ordered pairs are equal, corresponding elements are equal Hence x/3 1 = 5/3 x/3 = 5/3 – 1 x/3 = 2/3 x = 2 y – 2/3 = 1/3Algebra Graph y=1/3x3 y = − 1 3 x 3 y = 1 3 x 3 Rewrite in slopeintercept form Tap for more steps The slopeintercept form is y = m x b y = m x b, where m m is the slope and b b is the yintercept y = m x b y = m x b Write in y = m x b y = m x b form Tap for more steps
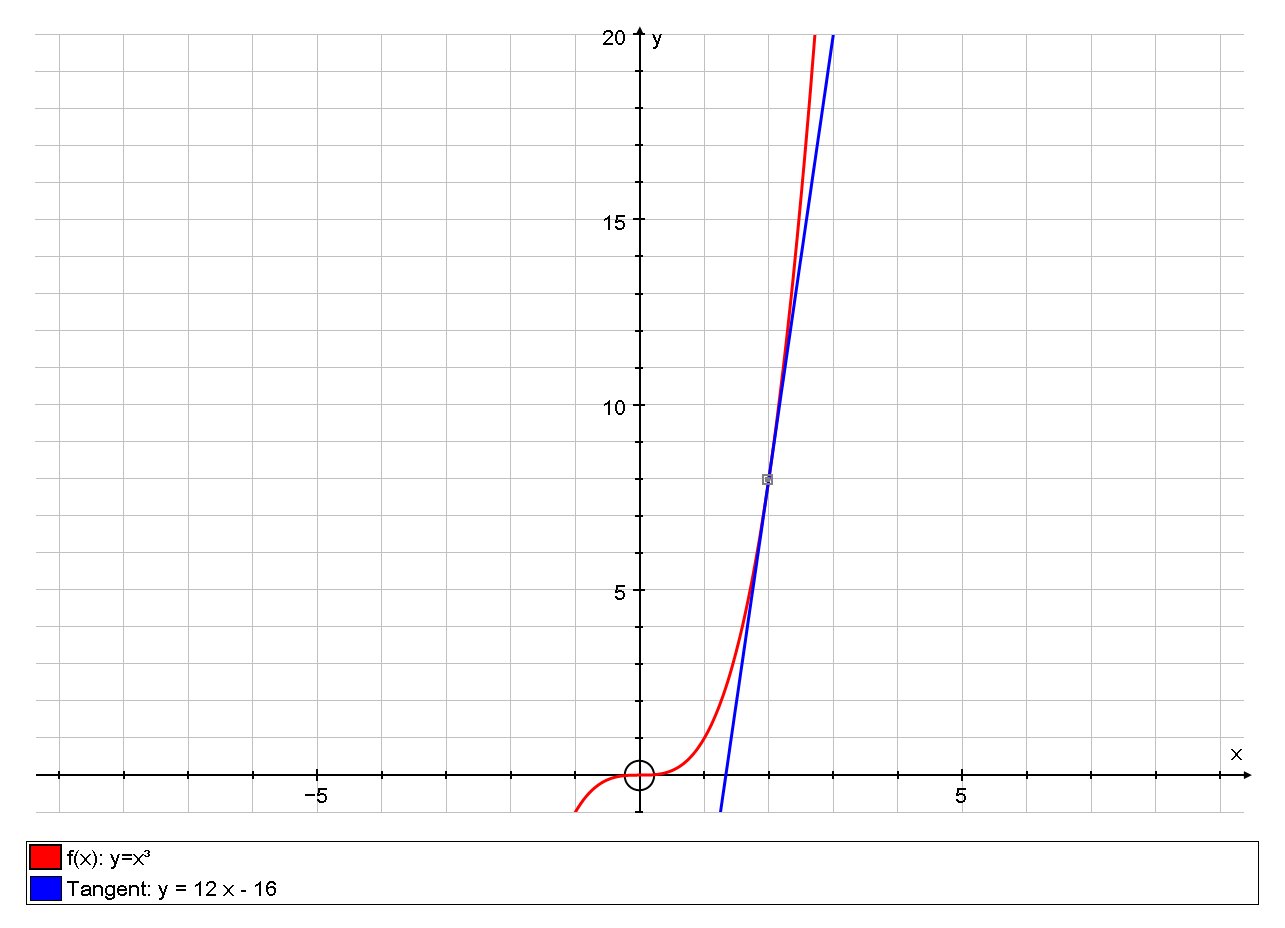



How Do You Find The Equation Of The Tangent Line To The Graph Of F X X 3 At Point 2 8 Socratic




7 Steps To Calculate Measurement Uncertainty Isobudgets
For y = 0,1,2,3;Then type x=6 Try it now 2x3=15 @ x=6 Clickable Demo Try entering 2x3=15 @ x=6 into the text box After you enter the expression, Algebra Calculator will plug x=6 in for the equation 2x3=15 2(6)3 = 15 The calculator prints "True" to let you know that the answer isY=3/2x2;y=1/2x2 Simple and best practice solution for y=3/2x2;y=1/2x2 Check how easy it is, to solve this system of equations and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework




Chapter P Prerequisites Manualzz




Ex 3 6 1 I And Ii Solve 1 2x 1 3y 2 1 3x 1 2y
Solve the given inequalities 3x y ≥ 12, x y ≥ 9, x ≥ 0, y ≥ 0graphically in two – dimensional plane asked Jul 22 in Linear Equations by KumarArun ( 13Simple and best practice solution for y3=2(x1) equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand,SOLUTION 1 Begin with x 3 y 3 = 4 Differentiate both sides of the equation, getting D ( x 3 y 3) = D ( 4 ) , D ( x 3) D ( y 3) = D ( 4 ) , (Remember to use the chain rule on D ( y 3) ) 3x 2 3y 2 y' = 0 , so that (Now solve for y' ) 3y 2 y' = 3x 2, and Click HERE to return to the list of problems SOLUTION 2 Begin with (xy) 2 = x y 1 Differentiate both sides




Curve Fitting And Solution Of Equation




Starter Algebraic Pyramid Challenge Ppt Download



1 2x 1 3y 2 And 1 3x 1 2y 13 6 Solve The Given Linear Equation By Substitution Method Sarthaks Econnect Largest Online Education Community



Solve The Following By Reducing Them To Quadratic Equations X 1 X 1 X X 13 6 Sarthaks Econnect Largest Online Education Community




Graph By Plotting Points



Link Springer Com Content Pdf m 3a978 1 4419 8532 3 2f1 Pdf




Curve Fitting And Solution Of Equation




The Sum Of X 1 And 2x Is 7 Solve For X How Can One Solve This Quora




Sqrt X 1 X Sqrt 1 X X 13 6 Youtube




Find The Equation Of The Circle Passing Through The Point 13 6 And Touching Externally The Two Circles X2 Maths Conic Sections Meritnation Com



Q Tbn And9gcr 1dgo8hvxswiukh8f1bnhr2y9gezqfzmkry8lclqvdowjtaba Usqp Cau




Solve The Problem 12 7 1 8 21 Let A 87 4 And Chegg Com




Solve For X And Y Using Cross Multiplication Method 2 X 1 3 Y 1 2 3 X 1 2 Y 1 13 6 Maths Pair Of Linear Equations In Two Variables Meritnation Com




3x 2 5y 3 2 And X 3 Y 2 13 6 Solve Using Substitution Method Youtube




Solve For X And Y X 1 2 Y 1 3 9 And X 1 3 Y 1 2 8 Brainly In




An Introduction To Glmnet Glmnet




Ex 3 6 1 I And Ii Solve 1 2x 1 3y 2 1 3x 1 2y




2 X 1 3 Y 1 2 3 X 1 2 Y 1 13 6 Brainly In




Solve X And Y 2x 3 3 Y 13 5 X 4 Y 2 Mathematics Topperlearning Com Ktrqykww




1 2x 1 3y 21 1 3x 1 2y 13 6 Solve The Above Linear Equations By Reducing Them To A Pair Of Linear Equations Mathematics Topperlearning Com Snootk99




Mrs Rivas Ppt Video Online Download




2 X 1 3 Y 1 2 3 X 1 2 Y 1 13 6 Find X And Y Brainly In



Solve The Following By Reducing Them To Quadratic Equations X 1 X 1 X X 13 6 Sarthaks Econnect Largest Online Education Community




Solve 2x 3 X 1 6 7x 1 4 13 6 Hence Find The Value Of A If 1 A 5x 8 Brainly In




Solve The Following Pairs Of Exations By Reducing Them To A Pair Of Linear Equations Begin Array Ll Text 1 Frac 1 2 X Frac 1 3 Y 2 Frac 2 Sqrt X Frac 3 Sqrt Y 2 Begin Array Ll Frac 1 3 X Frac 1 2 Y Frac 13




Oneill Janelle Redesigningabsolutevaluemethodology



1




1 2x 1 3y 2 1 3x 1 2y 13 6 Brainly In




Solve 5 Y 2 X 13 6 36 X 24 Y 1 Brainly In



1 2x 1 3y 2 And 1 3x 1 2y 13 6 Solve The Given Linear Equation By Substitution Method Sarthaks Econnect Largest Online Education Community
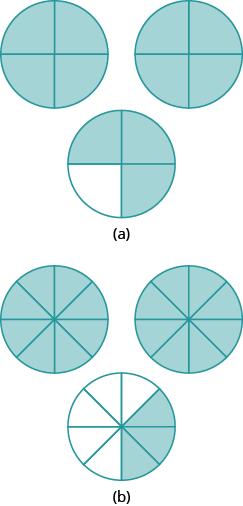



Problem Set 4 Fractions Prealgebra




Solve 5 Y 2 X 13 6 36 X 24 Y 1 Brainly In




Rd Sharma Solutions For Class 8 Chapter 1 Rational Numbers Download Free Pdf




Find The Value Of X And Y By Cross Multiplication Method Of 2 X 1 3 Y 1 2 3 X 1 2 Y 1 13 6 Brainly In




Rd Sharma Solutions For Class 8 Chapter 1 Rational Numbers Download Free Pdf




Pdf Optimizing Clifford Gate Generation For Measurement Only Topological Quantum Computation With Majorana Zero Modes Semantic Scholar




Ex 3 6 1 I And Ii Solve 1 2x 1 3y 2 1 3x 1 2y




1 2x 1 3y 2 1 3x 1 2y 13 6 Brainly In



Q Tbn And9gcr 1dgo8hvxswiukh8f1bnhr2y9gezqfzmkry8lclqvdowjtaba Usqp Cau



Solve The Following Pairs Of Equations By Reducing Them To A Pair Of Linear Equations I 1 2x 1 3y 2 Sarthaks Econnect Largest Online Education Community




Solve 5 Y 2 X 13 6 36 X 24 Y 1 Brainly In




2 3 11 Vi If A 1 2 2 Find A 1 And Hence Solve The System Of Equations 3 1 1 2x Y 3z 13 3x 2y Z 4 X 2y Z 8 1 1 27 2 0 11



Find The Value Of X And Y By Cross Multiplication Method Of 2 X 1 3 Y 1 2 3 X 1 2 Y 1 13 6 Brainly In




I Am Not Able To Understand The Deal With These Skew Lines Calculus



Problem Set 4 Fractions Prealgebra




If 2 X 3 4 1 1 2 X 1 5 Is A Singular Matrix Then X Is A 13 25 B 25 13 C 5 13 D 25 13




Curve Fitting And Solution Of Equation




Rd Sharma Solutions For Class 8 Chapter 1 Rational Numbers Download Free Pdf




Example 18 Solve 5 X 1 1 Y 2 2 6 X 1 3 Y 2 1 Examples
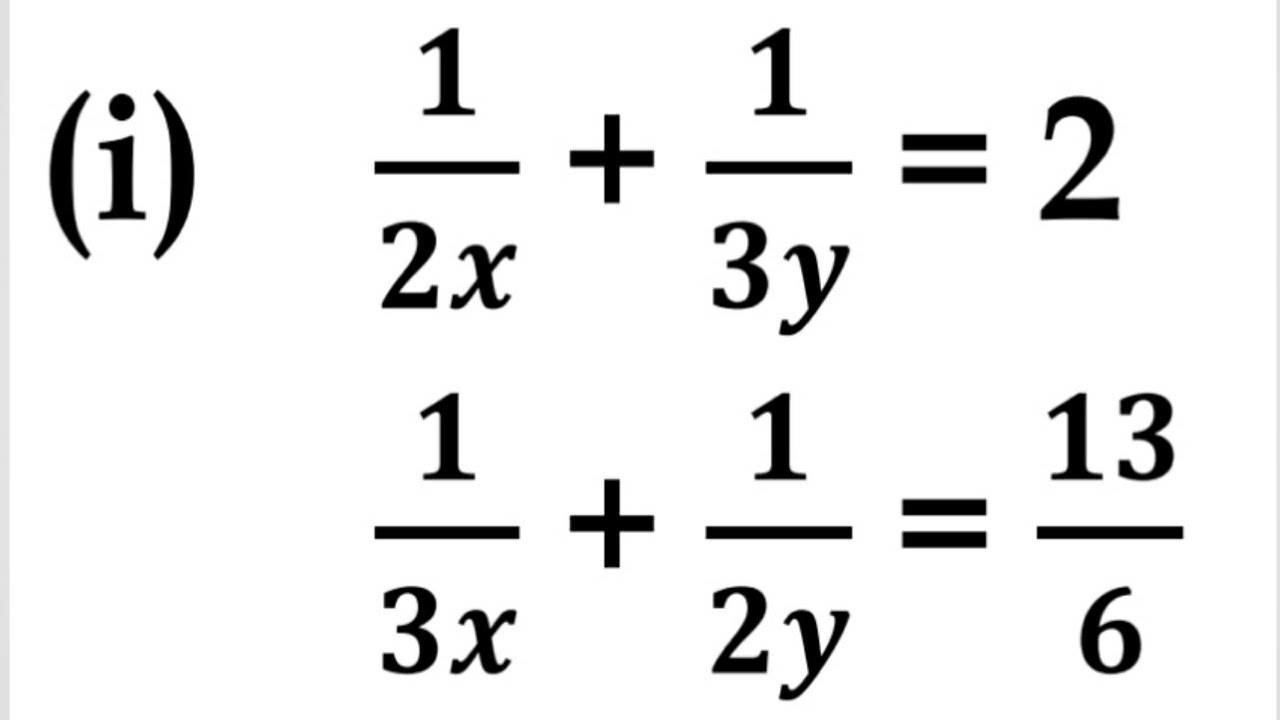



1 2x 1 3y 2 1 3x 1 2y 13 6 1 2x 1 3y 2 1 3x 1 2y 13 6 Rpk86 Youtube




Graph By Plotting Points




Phablet Wikipedia




2 X 2 3y 1 6 And 3 X 2 Y 0 Problem Set 1 Q6 1 Of Linear Equation In Two Variables Youtube




Solve The Following Pairs By Reducing Them To A Pair Of Linear Equation 1 2x 1 3y 21 3x 1 2y Brainly In




Solve For X And Y Using Cross Multiplication Method 2 X 1 3 Y 1 2 3 X 1 2 Y 1 13 6 Maths Pair Of Linear Equations In Two Variables Meritnation Com



2



Solve 5 X 1 1 Y 2 2 And 6 X 1 3 Y 2 1 Studyrankersonline



Solve 2 X 2 3y 1 6 And 3 X 2 Y 0 And Hence Find A For Which Y A X 4 Youtube




Solve The Following Pairs Of Equations By Reducing Them To A Pair Of Linear Equations V V M 3y 14 2 4y 23 W 72 2 5 X Vi 6x



1 2x 1 3y 21 1 3x 1 2y 13 6 Solve The Above Linear Equations By Reducing Them To A Pair Of Linear Equations Mathematics Topperlearning Com Snootk99




X 1 2 Y 1 3 8 X 1 3 Y 1 2 9 Simultaneous Linear Equation Brainly In




1 2x 1 3y 2 1 3x 1 2y 13 6 1 2x 1 3y 2 1 3x 1 2y 13 6 Rpk86 Youtube



Problem Set 4 Fractions Prealgebra




Ex 3 6 1 Iii Iv 4 X 3y 14 3 X 4y 23 Ex 3 6




1 2x 1 3y 2 1 3x 1 2y 13 6 Xand Y Is Not 0 Brainly In




Ex 3 6 1 I And Ii Solve 1 2x 1 3y 2 1 3x 1 2y




Starter Algebraic Pyramid Challenge Ppt Download




How To Find The Equation Of A Line 8 Steps With Pictures



Solve The Following Pairs Of Equations By Reducing Them To A Pair Of Linear Equations I 1 2x 1 3y 2 Sarthaks Econnect Largest Online Education Community




The Deubiquitinase Ubiquitin Specific Protease Is A Positive Modulator Of Myocardial B1 Adrenergic Receptor Expression And Signaling Journal Of Biological Chemistry
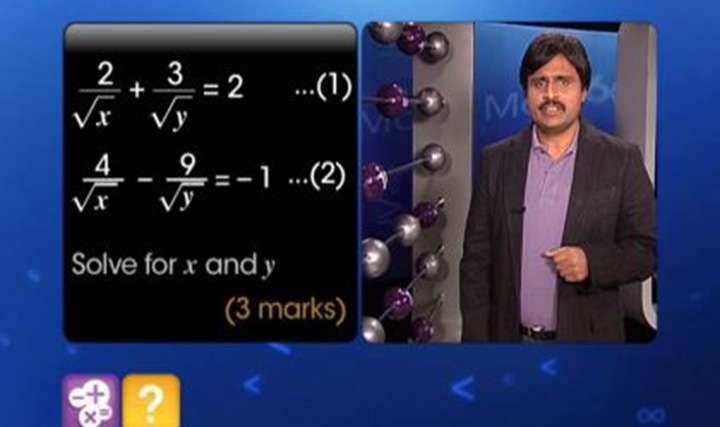



1 2x 1 3y 21 1 3x 1 2y 13 6 Solve The Above Linear Equations By Reducing Them To A Pair Of Linear Equations Mathematics Topperlearning Com Snootk99




Graph By Plotting Points




Curve Fitting And Solution Of Equation



V0icibbbwmrq0m




Incredible Math Secret How To Divide By 13 In Your Head Youtube




3x 2 5y 3 2 And X 3 Y 2 13 6 Solve Using Substitution Method Youtube




The Sum Of X 1 And 2x Is 7 Solve For X How Can One Solve This Quora




1 2x 1 3y 2 1 3x 1 2y 13 6 Solve The Pair Of Equations By Reducing Them To A Pair Youtube



0 件のコメント:
コメントを投稿